A change to make diffusion models 80% faster

There’s no shortage of excitement around diffusion models like DALL-E 2 and Stable Diffusion, and for good reason. These AI systems can generate stunning images from mere text descriptions, enabling everything from digital art to computer-aided design. But beneath the surface, there’s a dirty secret: diffusion models are notoriously slow and computationally intensive.

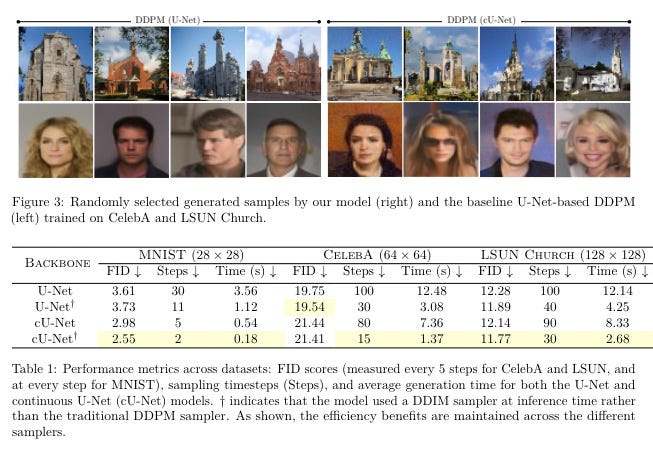
It sounds too good to be true, but that’s exactly what a team from Oxford, Cambridge, Imperial College London, and King’s College London are claiming in their latest paper. By completely rethinking a core component of diffusion models, they’ve achieved a seemingly impossible trifecta: faster, lighter, and better. They claim they can make models up to 80% faster while using 75% fewer parameters and a fraction of the memory.

If their approach pans out, it could be a watershed moment for diffusion models. Suddenly, the most powerful image and video synthesis models would be practical for a much wider range of applications, from mobile apps to real-time creative tools to robotic movement planning (yep!). And that’s just the beginning.

By the way, if you find technical news interesting, you should consider becoming a subscriber. You’ll get access to my complete analysis on trending papers like this one, where I break down the technical details, explore the strengths and limitations of the approach, and ponder the potential ripple effects on the field of generative AI.

Trust me, if you’re at all interested in the technical details of the AI revolution, you won’t want to miss this deep dive.

And if you know anyone else who geeks out about breakthroughs in deep learning, please share this post with them. The more minds we have buzzing over the implications of this research, the better.

Now, let’s dig in…

AIModels.fyi is a reader-supported publication. To receive new posts and support my work subscribe and be sure to follow me on Twitter!

Overview

The paper, titled “The Missing U for Efficient Diffusion Models,” introduces a new approach to designing the denoising U-Net architecture at the heart of diffusion models.

So what’s the secret? Two words: continuous U-Nets.

In a nutshell, the researchers have found a way to replace the notoriously slow and memory-hungry denoising process at the heart of diffusion models with a novel architecture that leverages calculus and dynamic systems. The result is a massive boost in efficiency, without compromising the quality we’ve come to expect from models like DALL-E and Stable Diffusion.

This might sound like a minor technical detail, but the implications are significant. By reformulating the U-Net in terms of calculus and differential equations, the researchers were able to create a model that is:

• Up to 80% faster during inference
• 75% smaller in terms of number of parameters
• 70% fewer FLOPs
• Able to achieve similar or better image quality with a fraction of the computational resources

In other words, they’ve found a way to make diffusion models practical for a much wider range of applications, from real-time creative tools to deployment on resource-constrained devices like smartphones.

Plain English Explanation

To understand why this matters, let’s start with a simple analogy. Imagine you’re an artist trying to paint a photorealistic portrait. But instead of starting with a blank canvas, you begin with a canvas covered in random splotches of paint.

Your job is to gradually refine those splotches into a recognizable image, one brushstroke at a time. The catch? You have to make thousands of tiny brushstrokes, and each one is dependent on the state of the canvas at the previous step, which is slow because you have a lot of wasted motion.

This is essentially what the denoising U-Net in a diffusion model does. It starts with a “noisy” latent representation and progressively removes the noise over many iterations, slowly homing in on the target image. The problem is that this iterative process is incredibly time-consuming and memory-intensive, even for today’s most powerful GPUs.

What the researchers have figured out is a way to model this denoising process continuously, using the language of calculus and differential equations. Instead of having to make thousands of tiny brushstrokes, their model can describe the entire denoising trajectory as a single, smooth curve. It’s a bit like being able to paint with a giant brush that automatically refines itself as you go.

The end result is a model that can denoise images much faster and more efficiently, without sacrificing quality. And because the model is so much smaller in terms of number of parameters, it’s much more practical to deploy on a wide range of devices and platforms.

Technical Explanation

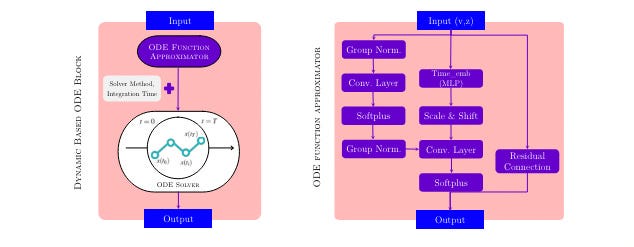
Now let’s dive into the technical details. The core idea of the paper is to replace the standard discrete U-Net architecture in a diffusion model with a continuous U-Net that leverages techniques from neural ODEs.

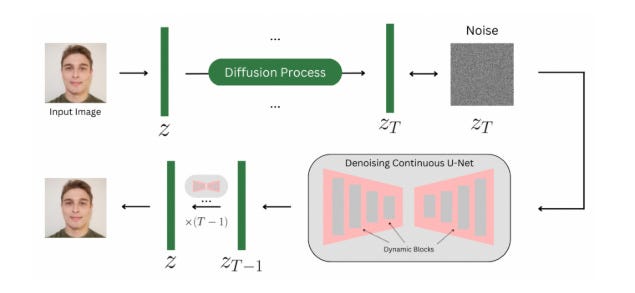
The key components of this new architecture are:

• A dynamic neural ODE block that models the evolution of the latent representation over time using a second-order differential equation of the form: d²x/dt² = f(x, dx/dt, t), where f is parameterized by a neural network
• Adaptive time embeddings that allow the model to condition the dynamics on the current diffusion timestep
• A numerical ODE solver that efficiently integrates the dynamics function to generate the denoised output
• A constant-memory adjoint method for backpropagating gradients through the ODE solver during training

The continuous U-Net is trained end-to-end as part of the overall diffusion model framework, learning to approximate the reverse diffusion process from noisy latents to clean images. The key difference is that the denoising trajectory is modeled continuously, rather than as a fixed sequence of discrete steps.

In the paper, the authors provide a detailed mathematical analysis of why this continuous formulation leads to faster convergence and more efficient sampling. They also conduct extensive experiments on standard image generation benchmarks, demonstrating significant improvements in inference speed and parameter efficiency compared to state-of-the-art discrete U-Net architectures.

Critical Analysis

While the results presented in the paper are impressive, there are a few caveats and limitations worth noting.

First and foremost, the continuous U-Net architecture introduces additional complexity in the form of the ODE solver and adjoint method. These components can be tricky to implement efficiently, especially on hardware accelerators like GPUs. The authors use a third-party ODE solver library in their experiments, which may not be optimized for the specific use case of diffusion models.

Second, the experiments in the paper focus primarily on image super-resolution and denoising tasks, which are somewhat simpler than full-scale image generation. It remains to be seen how well the continuous U-Net approach scales to more complex datasets and higher resolutions.

Finally, while the efficiency gains are impressive, diffusion models will likely still require significant computational resources even with the proposed improvements. Making these models truly practical for on-device deployment may require additional innovations in areas like network pruning, quantization, and hardware acceleration.

That being said, the potential implications of this work are hard to overstate. If the efficiency gains can be realized in practice, it would open up a whole new range of applications for diffusion models, from real-time video synthesis to 3D scene generation. It could also inspire further research into other ways of incorporating continuous dynamics into deep learning architectures.

Conclusion

In conclusion, “The Missing U for Efficient Diffusion Models” represents a big step forward in making generative AI more practical and accessible. By leveraging techniques from neural ODEs and continuous dynamical systems, the authors have demonstrated that it’s possible to achieve substantial improvements in speed and parameter efficiency without sacrificing image quality.

If this approach can be scaled up and optimized further, it could bring the power of diffusion models to a much wider audience.

Perhaps more importantly, this work opens up exciting new avenues for further research at the intersection of deep learning, differential equations, and dynamical systems. It hints at the possibility of a more unified mathematical framework for understanding and designing neural networks, one that blurs the lines between discrete and continuous computation.

Of course, realizing this vision will require close collaboration between experts in machine learning, numerical analysis, and applied mathematics. But if this paper is any indication, the payoff could be huge.

As a final thought, it’s worth reflecting on the broader societal implications of this kind of research. As generative AI models become more efficient and widely deployed, we’ll need to grapple with thorny questions around issues like intellectual property, misinformation, and all sorts of other AI ethics questions. Ensuring that these powerful tools are developed and used responsibly will be one of the great challenges of the coming decades.

In the meantime, I’m excited to see where this line of work leads. If you’re as fascinated by the frontiers of AI as I am, I encourage you to dive into the comments and share your thoughts.

And if you found this analysis valuable, please consider subscribing to support my work. I’ll be keeping a close eye on this space using the top papers view over on the site and sharing my perspectives on the latest breakthroughs.

As always, thanks for reading!

AIModels.fyi is a reader-supported publication. To receive new posts and support my work subscribe and be sure to follow me on Twitter!