Tsinghua University: Inverting Transformers Significantly Improves Time Series Forecasting

Transformers have become the dominant model architecture for natural language processing and computer vision applications. However, recent research has revealed that standard Transformer-based models struggle to match the performance of even simple linear models on time series forecasting tasks.

In this post, we'll look at the rise of Transformers, discuss in detail why they underperform in forecasting, and walk through a new paper from Tsinghua University and Ant Group that proposes a simple but impactful tweak to Transformer architecture that yields state-of-the-art forecasting results.

Subscribe or follow me on Twitter for more content like this!

The Rise of Transformers

Transformers were first introduced in 2017 and swiftly became a staple of natural language processing, achieving new state-of-the-art results across tasks like translation, summarization, and question-answering.

The Transformer architecture relies entirely on attention mechanisms instead of recurrence like LSTMs. This allows models to draw global dependencies between elements in a sequence, rather than process sequentially. Transformers also benefit from more parallelizability during training.

Given the immense success of Transformers on sequence modeling for language, it was natural that researchers began exploring their potential on time series data as well. Time series forecasting is crucial for applications like demand prediction, infrastructure monitoring, and financial analysis.

Many papers proposed adapted Transformers for univariate and multivariate time series forecasting. Modifications typically focused on the attention mechanism itself or adding specialized components like temporal convolutions.

However, it turns out directly applying Transformers to time series data results in underwhelming performance compared to expectations set by language tasks.

The Problem with Transformers for Time Series

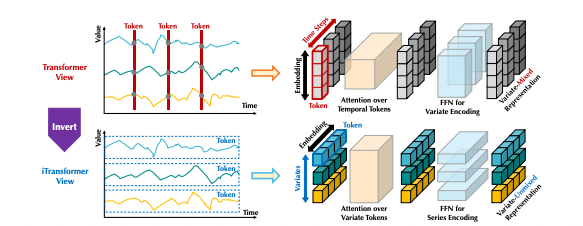
Most Transformer architectures for time series embed each timestamp as a token, fusing all variable values recorded at that time step. Attention is then applied to model dependencies between these timestamp tokens.

This approach has two main weaknesses when applied to forecasting:

1. Misaligned multivariate data - Real-world time series often have misaligned timestamps across variables. Sensors record at slightly different times, server metrics are logged asynchronously, etc. Fusing all variables into one timestamp token eliminates temporal offset information and introduces noise.
2. Limited receptive field - Each timestamp token can only access a single moment in history. Forecasting typically requires a much longer input sequence, but standard self-attention over timestamps has no ability to model long-range dependencies.

Due to these issues, Transformers struggle to extract useful representations of time series dynamics. They fail to effectively leverage historical context or model relationships between distinct variables.

Recent linear models like Gaussian Processes and LSTMs with linear layers have shown stronger empirical performance on forecasting tasks as a result. Many have begun to question if attention mechanisms provide any benefit to time series modeling versus simply using linear regressors.

Introducing the Inverted Transformer

A new paper from Tsinghua University proposes a different perspective - instead of lackluster performance being inherent to Transformers, it is caused by improperly applying the architecture to time series data.

They introduce the inverted Transformer, or iTransformer, which swaps the roles of key components in the standard Transformer encoder:

• Time series as tokens - The entire history of each variable is embedded as a standalone token, rather than fusing variables together per timestamp.
• Self-attention on variables - Attention is applied to the variable tokens to model relationships between different time series.
• Feedforward on time - Feedforward networks process each variable token independently to extract temporal representations.

This simple inversion aligns the architecture with the nature of forecasting data - attention detects correlations between misaligned variables, while feedforward layers model each temporal sequence.

Benefits of the Inverted Architecture

The authors empirically demonstrate that this inverted Transformer achieves state-of-the-art results across many forecasting benchmarks. The improvements stem from several advantages:

• Multivariate modeling - Attention over full series tokens better captures dependencies between variables. The authors visualize attention maps that clearly highlight relationships.
• Generalization - Feedforward networks extract shared patterns across time series, enabling generalization to unseen variables at test time.
• Receptive field - Full series tokens provide complete historical context to the model. The authors show linear-like benefits from increasing the input sequence length.
• Interpretability - Inverted attention maps are more coherent compared to timestamp attention, aiding understanding.

Furthermore, the approach consistently boosts performance when applied to efficient Transformer variants. This helps resolve the quadratic complexity issue arising from many variables.

Key Takeaways

The paper provides compelling evidence that Transformers can in fact achieve state-of-the-art time series forecasting performance, but only if the architecture is adapted to the unique structure and needs of forecasting tasks.

Rather than overly complex modifications, simply inverting the roles of the Transformer's core modules results in significantly stronger modeling ability and generalization. Beyond forecasting, the work highlights the importance of inductive biases that align neural architectures with the underlying data characteristics.

The iTransformer model offers a promising new foundation for time series learning based on the strong capabilities of the Transformer. The gains in accuracy, efficiency, and interpretability make this simple but clever architectural inversion worthy of further exploration across forecasting and related sequential predictive tasks.

Subscribe or follow me on Twitter for more content like this!