Tool-Integrated Reasoning: A New Approach for Math-Savvy LLMs

Mathematical reasoning has long been a challenging frontier for artificial intelligence. While language models like GPT-3 and ChatGPT have achieved impressive performance on many language tasks, they still struggle to solve complex university-level math problems accurately. Mastering sophisticated mathematical reasoning capabilities could unlock AI applications in diverse fields like science, engineering, finance, and more.

Recently, researchers from Tsinghua University and Microsoft made significant progress in strengthening the mathematical reasoning skills of large language models. Their key technical innovation (presented here) is integrating external mathematical tools like computational libraries and symbolic equation solvers directly into the models' reasoning process.

Let's see how it works!

Subscribe or follow me on Twitter for more content like this!

The Problem: Why Math Remains Difficult for Language Models

Tasks like numerical calculation and basic algebra can be handled reasonably well by existing models. However, complex mathematical problem solving involving multi-step inference, symbolic manipulations, and abstract concepts remains problematic.

For instance, models often fail to solve algebra word problems that require identifying variables, setting up systems of equations, and mathematically formalizing relationships described verbally in text. Geometry poses challenges due to the need for spatial reasoning skills. High school and university math exercises also introduce concepts like proofs, integrals, matrices, and more that confound existing language models.

The researchers attribute these difficulties to two main factors:

• Lack of abstract reasoning capabilities: Language models today are trained primarily on internet text corpora. While this teaches linguistic skills, it does not provide the structured knowledge and logic needed for mathematical reasoning.
• Inability to perform symbolic computations: Language lacks the rigor and precision required for manipulating mathematical symbols. Models may make small errors in each step that accumulate over multi-step problems.

Tool-Integrated Reasoning: A New Training Paradigm

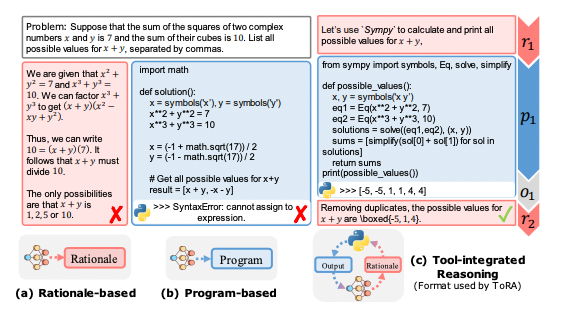
To address these challenges, the researchers propose teaching language models to reason in a format they term Tool-Integrated Reasoning. The key innovation is interleaving natural language rationales generated by the model with code to invoke external mathematical tools.

For example, given a complex algebra word problem, the model may first describe the approach in words, then write a Python program using SymPy to symbolically set up the system of equations, execute it to get a solution, and finally explain the result verbally.

This complements the strengths of language models in high-level reasoning and planning with the precision and computational power of mathematical tools. The anticipate this could significantly enhance the models' ability to solve problems requiring both semantic understanding and symbolic manipulation.

Training Methodology: Imitation Learning from Tool Interaction Examples

To realize this vision, the researchers first had to create a dataset demonstrating tool-integrated reasoning on math problems. They leveraged the capabilities of GPT-3 to automatically generate 16,000 examples of GPT-3 itself solving problems from the GSM8k and MATH datasets while interacting with tools like SymPy.

With this corpus of tool interaction trajectories, the team pre-trained versions of the LLaMA model using imitation learning. That is, the models were trained to predict the tool usage behavior and interleaved natural language rationales demonstrated in the dataset.

This approach produced a series of Tool-integrated Open-source Reasoning Agents (TORA) ranging from 7 billion to 70 billion parameters.

Significant Performance Improvements on Math Reasoning

The researchers systematically evaluated the TORA models on 10 diverse mathematical reasoning datasets and compared performance to prior state-of-the-art techniques.

The results demonstrate that tool-integrated reasoning training yields substantial gains across model sizes and tasks:

• TORA models achieved 13-19% higher accuracy on average compared to the best existing open-source models.
• On a challenging competition-level math test (MATH dataset), TORA-7B scored 40% accuracy, beating the previous best model by 22 percentage points absolute.
• TORA-34B attained 51% accuracy on MATH, surpassing GPT-4's performance of 43% on the same problems.

This suggests that learning to leverage external tools could notably enhance even very large models like GPT-4 at mathematical reasoning.

Interestingly, the improvements were consistent across diverse problem types spanning arithmetic, algebra, calculus, geometry, probability, etc. Tool integration appears to provide broad benefits.

Analysis Reveals Complementary Strengths of Language and Tools

To better understand model behavior, the researchers systematically analyzed tool usage patterns across mathematical domains:

• For algebra problems, models predominantly used symbolic tools like SymPy to manipulate equations. This aligned well with the need for rigorous, precise symbolic calculations.
• In numeric domains like probability, models relied more heavily on algorithms for computations like factorials.
• For geometry, applying tools provided smaller gains, indicating spatial reasoning remains a challenge.

They also evaluated ablations removing either natural language rationales or tool integration:

• Tool interaction consistently outperformed models using only programming or only natural language across problem types.
• Rationales provided the largest benefits for geometry, algebra and precalculus - domains requiring high-level planning and reasoning.

These insights illuminate the complementary strengths of both linguistic and symbolic reasoning.

Limitations and Open Problems

Despite the gains from tool integration, significant room for improvement remains. The researchers identified geometry and advanced algebra as areas where models still struggled.

Geometry poses a challenge as current tools like SymPy have limited capabilities for spatial reasoning. Advances in multi-modal reasoning and tighter integration with graphical libraries could help.

For abstract algebra, techniques used by human mathematicians like leveraging known theorems and working problems backwards from the result may be needed. Stronger symbolic reasoning capabilities are also likely required.

Overall, this research provides promising evidence that combining language model strengths with specialized external tools can notably improve mathematical reasoning. However, efficiently integrating different reasoning modalities and higher-level mathematical problem-solving strategies remains an open problem. These are important directions for future work.

The tool-integrated training paradigm introduced here could also spur investigation into integrating external capabilities to enhance reasoning across disciplines like logic, commonsense reasoning, and art. This could be an important step toward more capable and versatile AI systems.

Subscribe or follow me on Twitter for more content like this!