Format your data like this to dramatically improve your LLMs' math skills

Arithmetic is an important yet challenging domain for LLMs. While they have achieved tremendous success in natural language, their performance on arithmetic is often lacking. In this blog post, we'll summarize a recent technical paper that dives deeper into transformers' capabilities and limitations with arithmetic. Key findings include a new insight into positional encoding and techniques to enhance models' multiplication and addition skills. Let's begin!

Subscribe or follow me on Twitter for more content like this!

The Core Challenges of Arithmetic for Transformers

The paper begins by outlining three key challenges of arithmetic tasks for transformers:

1. Complicated calculation: Multiplication, especially of large numbers, requires intermediate steps that are difficult for transformers to perform internally without explicitly expressing each step externally.
2. Length extrapolation: Arithmetic exhibits highly regular patterns that models often learn by leveraging position information. However, relying solely on positional encodings prevents models from generalizing to numbers longer than those seen during training.
3. Integration with language: Simply combining arithmetic training data with natural language contextual data is not sufficient, as differing surface formats between the two domains can encourage position-dependent representations that conflict across domains. Differences in data representation may hinder effectively applying arithmetic skills regardless of the presentation format.

Enhanced Multiplication via Padding and Reordering

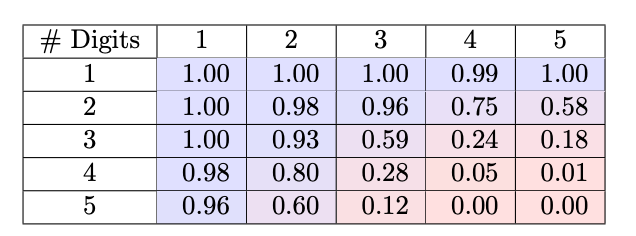
To empirically investigate techniques for strengthening models' multiplication capabilities, the paper focuses on assessing transformers' ability to directly output large number products. Traditionally, transformers struggle with this task, often only able to handle problems up to 4 digits at most.

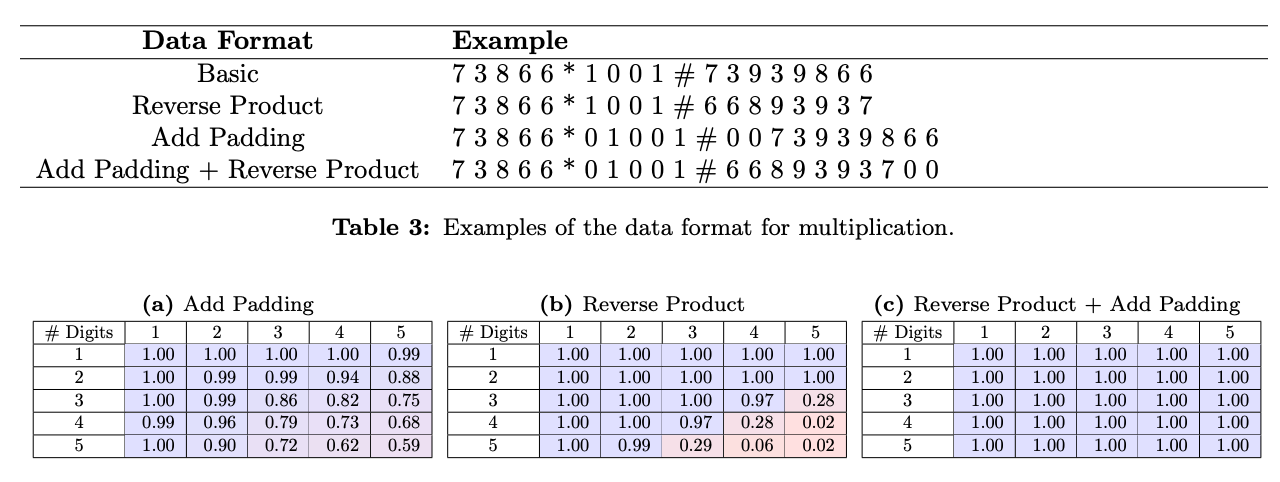
The researchers designed two targeted preprocessing modifications to standardize the format of the multiplication task. First, they padded all number factors to a fixed 15-digit length, eliminating variability in where the product position falls relative to the numbers. This transforms the inputs into uniform, position-invariant representations.

Second, they reversed the order of digits in the product. Why might this help? In multiplication, we begin by considering the least significant digits first before working our way to the most impactful digits. By inverting the product, the model sees an ordering that mirrors this natural progression.

With these normalized representations, the team trained a small 124M parameter GPT-2 model on 300k randomly sampled 1-15 digit multiplications. The results were dramatic - the model achieved over 99% accuracy in directly calculating products for numbers up to 12 digits long, a substantial improvement over baselines struggling past 4 digits.

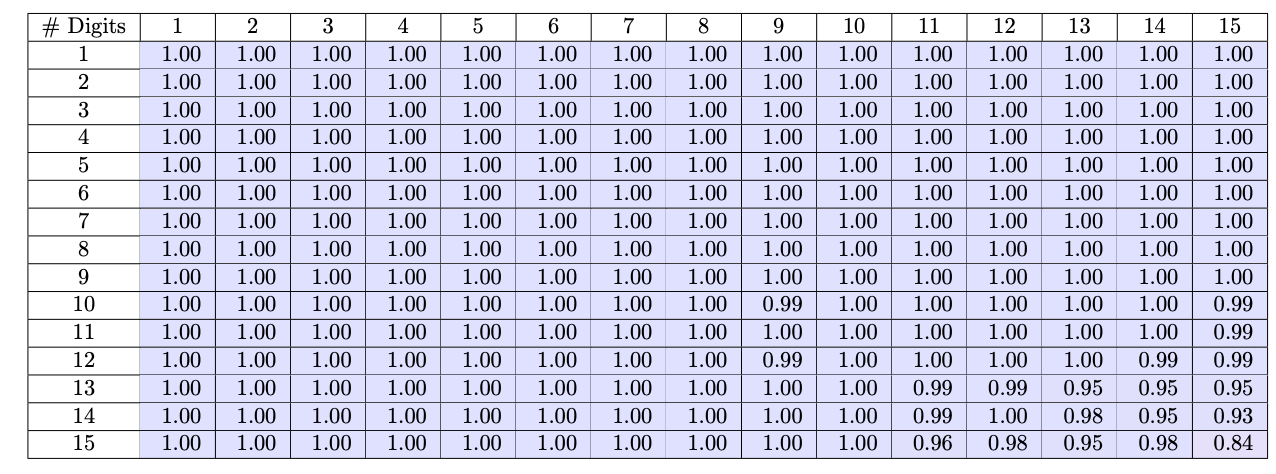
What does this demonstrate? By standardizing patterns and presenting the task in a more intuitive way, the model could recognize and apply the core rules of multiplication much more successfully than before, even for complex multi-digit calculations handled internally without verbose step-by-step workflows. The techniques helped uncover significant untapped computational potential within the transformer architecture for arithmetic reasoning.

Generalization to Longer Additions

To address length extrapolation, the paper studies data formats and positional encodings. Formats disrupting reliance on absolute position, like random spacing, helped models generalize addition up to 1-2 extra digits compared to standard formats. Recursive formats providing more contextual information per step aided generalization even further.

Alternative positional encodings like random embedding also boosted generalization by up to 13 digits by encouraging models to differentiate positions without absolute encodings. This suggests modified encodings and data representations can help models learn arithmetic concepts rather than surface patterns.

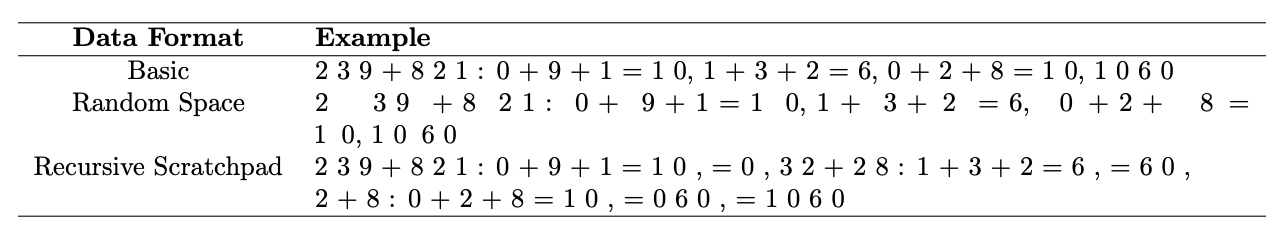
Integrating Arithmetic and Language

The paper examines if training models on pure arithmetic data helps when tasks appear in natural language. Naively combining the two led to little benefit due to differences in format. However, randomizing formats or using alternatives to absolute positional encoding successfully integrated the data, enabling transfer of arithmetic skills to language contexts.

This provides insight into how to build models that can fluidly apply arithmetic knowledge regardless of presentation, highlighting the importance of representation for learning fundamental mathematical concepts.

In summary, the paper gives valuable new understanding of transformers' arithmetic abilities and limitations. Key takeaways are techniques to enhance multiplication and generalization capabilities, as well as factors like positional encoding and representation affecting the integration of arithmetic and language. With further work, these findings could help develop improved models proficient across both domains.

Subscribe or follow me on Twitter for more content like this!