Anomaly Detection in Multivariate Time Series with... Diffusion Models?

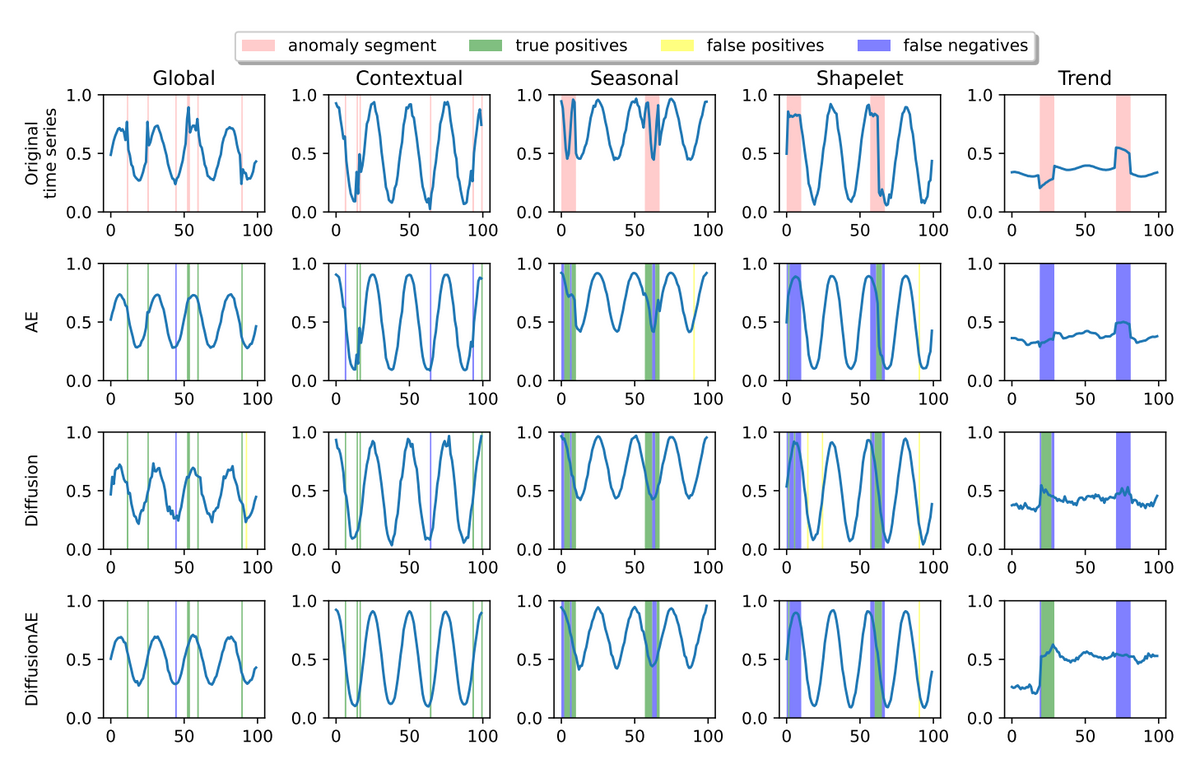
Multivariate time series anomaly detection is critical in fields ranging from healthcare and finance to cybersecurity and industrial surveillance. Spotting these anomalies can highlight significant events such as health conditions, fraudulent activity, cyber threats, or equipment malfunctions. As IoT devices and high-frequency data collection become more prevalent, the need for robust anomaly detection models for multivariate time series has become essential.

Deep learning methods have made significant strides in this area. Autoencoders, Generative Adversarial Networks (GANs), and Transformers are just a few of the approaches that have demonstrated effectiveness in identifying anomalies within time series data. A recent piece I shared discussed the innovative application of "inverted transformers" (iTransformers) in time series analysis, which you can read more about here.

However, a new twist emerged with my latest find—a new research paper on the use of diffusion models for time series data analysis. These models are best known for their impressive results in image and audio generation tasks, as evidenced by Stable Diffusion for images and AudioLDM for audio. They've even been applied to help robots adapt to complex environments, which you can learn about here.

This raises a compelling question: Can diffusion models be as effective for analyzing time series data? This post will examine the recent paper that has brought this question to the forefront, and we'll assess the viability of diffusion models in this specialized domain. Let's get started.

Subscribe or follow me on Twitter for more content like this!

The Promise and Limitations of Existing Methods

Traditional anomaly detection methods such as One-Class SVMs—a machine learning technique that surrounds normal data points with a decision boundary to identify anomalies—and Isolation Forests—an algorithm that detects outliers by isolating observations—are adept at handling individual data points in isolation. However, they don’t take into account the temporal relationships, the interconnected sequences of data that unfold over time, which are crucial for understanding evolving contexts within the dataset.

Deep learning models, by design, are more attuned to these sequential dynamics. Autoencoders, for instance, are neural networks trained to condense normal data into a compact representation during training and then reconstruct it during testing. Anomalies are flagged by measuring the reconstruction error, which is the disparity between the original data and its reconstructed version from the autoencoder; a significant error suggests an anomalous event.

Generative Adversarial Networks (GANs), composed of two neural networks—the generator and the discriminator—compete in a game-like setting. The generator creates new data instances while the discriminator assesses them, assigning likelihood scores that reflect the probability of a data instance being real. Anomalies are identified when the discriminator assigns low likelihood scores, indicating the data might not be genuine.

Transformers, a newer addition to the deep learning arsenal, leverage self-attention mechanisms, allowing the model to consider the entire sequence of data to understand the weight and significance of each part. This approach has led to state-of-the-art results in recognizing complex temporal correlations within time series data. However, these models can sometimes reconstruct anomalies with too much accuracy, which can be a drawback as it makes anomalies less discernible. Additionally, GANs are susceptible to mode collapse, where the generator starts producing limited and often repetitive outputs, reducing the model's ability to generalize and detect a wide range of anomalies.

Despite their promise, these deep learning techniques still face the challenge of consistently identifying anomalies across various datasets due to the complexity of modeling temporal dependencies and the inherent limitations of each approach.

Diffusion Models - A New Approach

Diffusion models are a novel class of deep generative models initially recognized for their prowess in generating detailed images. Their approach entails a gradual addition of noise to the data, which the model learns to reverse, effectively enabling it to eliminate noise and reconstruct high-resolution samples.

In the context of time series anomaly detection, this paper posits an intriguing hypothesis: diffusion processes may be particularly effective at smoothing out normal patterns while amplifying the irregularities in anomalies. If this holds true, it would result in a greater disparity between the original anomalous sequences and their reconstructed versions, thereby improving the identification of anomalies.

A diagram in the paper visually explains this theory, depicting how, through iterative rounds of noise addition and subsequent removal, anomalies become more pronounced when compared to their denoised versions. This amplification facilitates the differentiation of anomalous data from the norm post-diffusion.

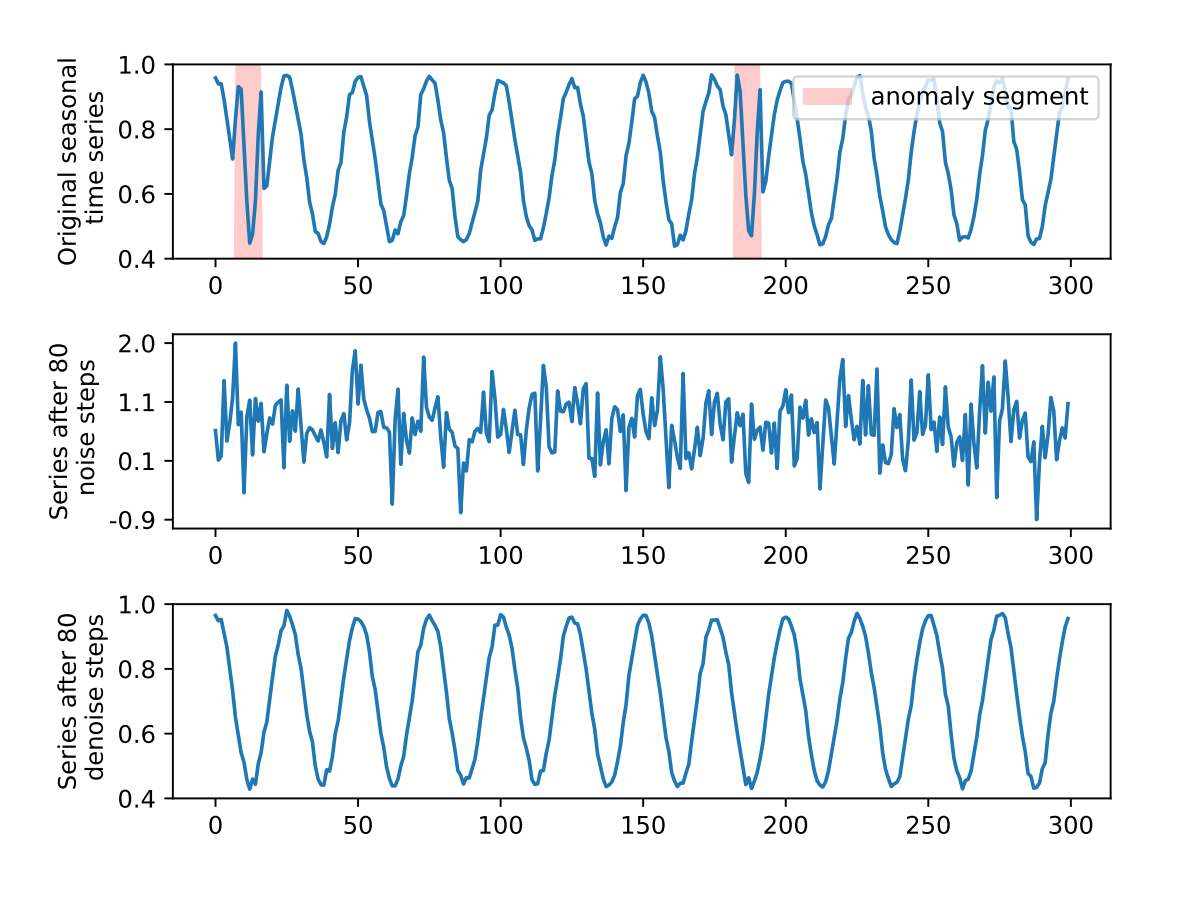
For practical implementation, the model undergoes training on multivariate time series data corrupted with Gaussian noise. In the testing phase, this process is mimicked by adding noise to new input sequences, which the model is then tasked to denoise. The difference between the original sequence and its denoised counterpart is quantified to produce an anomaly score.

The paper examines two variants of diffusion models applied to time series data:

1. A straightforward application where the diffusion model processes the raw time series input.
2. An enhanced "DiffusionAE" model, which employs an autoencoder's output as the preliminary input for the diffusion process.

The second approach, "DiffusionAE," enhances the diffusion model's robustness to inherent noise in the data by utilizing the autoencoder's capability to pre-filter noise. The comprehensive methodology is depicted in a diagram that outlines the entire pipeline, from the introduction of noise to the generation of the anomaly score.

Experimental Setup and Results

The models underwent rigorous testing on both synthetic and authentic multivariate time series datasets, which included a variety of anomaly types. These types were classified according to a recognized taxonomy:

• Point anomalies: Singular data points that are unusual compared to the rest.
• Contextual anomalies: Points that are abnormal when considered within their specific context.
• Seasonal anomalies: Irregular patterns that disrupt the expected cyclical trends.
• Shapelet anomalies: Anomalies within a subsequence or 'shapelet' in the time series.
• Trend anomalies: Points where the trend's direction sharply deviates from the established pattern.

For the synthetic datasets, anomalies were injected at predetermined ratios to maintain control over the experimental conditions. The real-world datasets comprised data recorded from sensors at a water treatment facility, adding a layer of complexity and unpredictability to the analysis.

Evaluating Anomaly Detection: Beyond Traditional Metrics

Traditional evaluation methods for time series anomaly detection, like the point-adjustment protocol, can misrepresent a system’s performance by producing high F1-scores even if only a single point in an anomalous segment is identified. Recognizing this, researchers in a recent paper have proposed more stringent evaluation protocols.

The P A%K protocol emerges as a solution, where 'K' represents the minimum percentage of points that must be detected within an anomalous segment for it to be considered correctly identified. This method ensures that models are recognized not just for detecting anomalies but for the extent of their detection capabilities.

Building on this, the researchers introduce the F1K-AUC metric, which calculates the area under the curve of F1-scores at various levels of 'K', offering a comprehensive perspective on a model's precision and recall across different stringencies of detection.

To further refine evaluation, the paper suggests using a modified ROC curve that accounts for true and false positive rates across multiple detection thresholds and 'K' values. This gives rise to the ROCK-AUC metric, which facilitates the comparison of anomaly detection models without the influence of threshold bias.

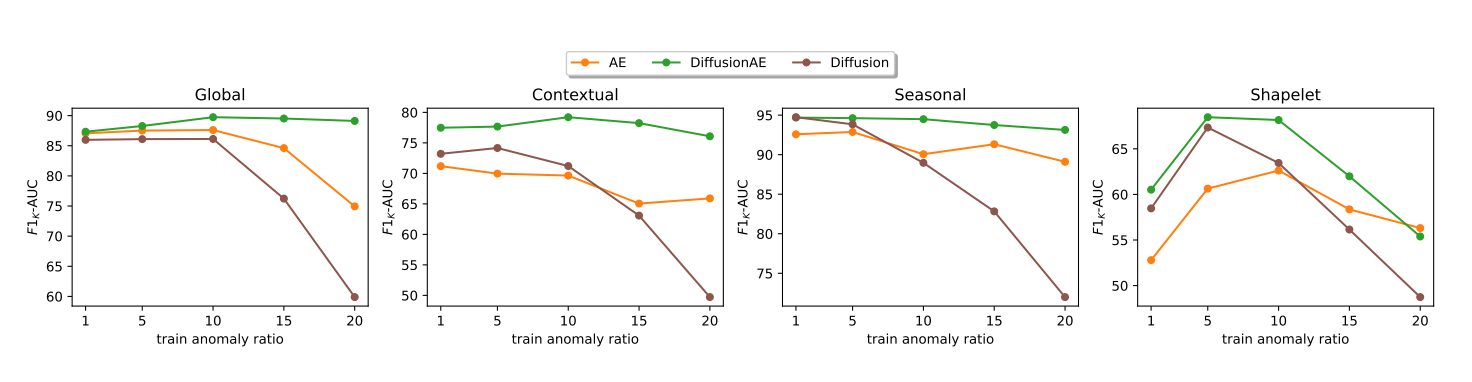
This shift in evaluation metrics aims to ensure that high scores in anomaly detection are indicative of genuine, robust model performance across varying degrees of anomaly detection challenges.

Key Takeaways and Future Work

The paper presents an in-depth analysis of anomaly detection in multivariate time series data, which is increasingly critical in various fields such as healthcare, finance, cybersecurity, and industrial monitoring. Detecting anomalies is key to identifying significant disruptive events, from health issues to fraud, cyber threats, and equipment malfunctions. Given the rise of IoT and high-frequency data collection, the demand for effective anomaly detection models for multivariate time series is more pressing than ever.

One of the paper's significant contributions is the exploration of deep learning methods, including autoencoders, GANs, and Transformers, which have already shown promise in identifying anomalies. It builds on this by proposing the use of diffusion models—more commonly associated with image and audio generation—for time series analysis. The central hypothesis is that diffusion processes might uniquely amplify the anomalies against normal patterns, enhancing detectability.

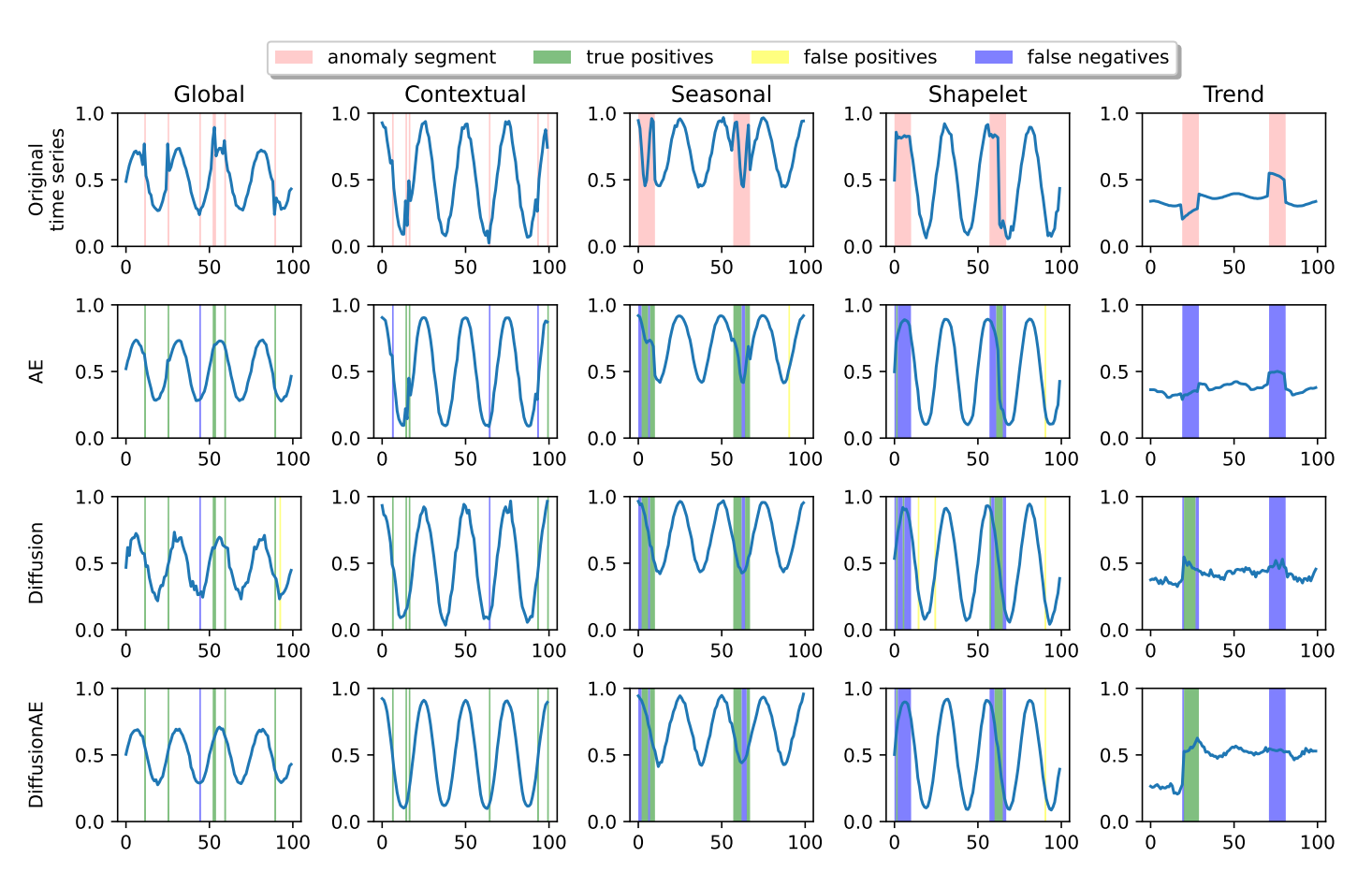
To address the inadequacies of traditional evaluation methods, the paper introduces more robust metrics, such as F1K-AUC and ROCK-AUC. These metrics aim to provide a more accurate assessment of an anomaly detection system's capabilities, ensuring that high scores are truly indicative of superior performance. The experimental results, obtained from testing on synthetic and real-world datasets, show that the DiffusionAE model, which combines an autoencoder with diffusion processes, exhibits notable robustness and efficacy.

Despite these promising results, the paper does mention the limitations inherent in the approach. For instance, the models, while successful on controlled synthetic data, encounter greater challenges with complex real-world datasets. This points to the need for further refinement to enhance the models' applicability in real-world scenarios.

Moreover, while the paper advocates for sophisticated evaluation metrics, these come with their own set of complexities and may require broader validation within the scientific community. Another point of concern is the generalizability of the models across diverse domains and types of anomalies—a common hurdle in machine learning. Lastly, the computational intensity of diffusion models could potentially limit their use in large-scale or real-time applications.

In summary, the paper underscores the potential of diffusion-based models in transforming the landscape of time series anomaly detection and calls for continued research to optimize these models for practical, varied applications. It also highlights the necessity for the adoption of advanced evaluation metrics to truly measure and understand the performance of anomaly detection systems.

Subscribe or follow me on Twitter for more content like this!